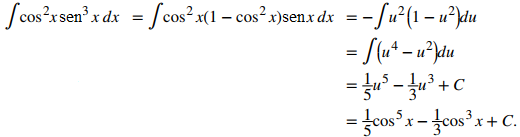Introducción.-
Cuando tratamos acerca del cálculo hay que saber que este tiene una condición muy importante para poder dominarlo, y es que se debe estar familiarizado con materias fundamentales como el álgebra y la trigonometría ya que después de todo, cada tema nuevo dentro de las matemáticas se viene construyendo sobre temas que se han visto anteriormente, ahora bien, es importante tomar en cuenta los conceptos de estas dos materias importantes con las que el cálculo está relacionado. La primera es el álgebra; una rama de las matemáticas que utiliza no solo números y signos, sino también letras para resolver operaciones y que busca hallar el valor numérico de variables denominadas incógnitas, las cuales se representan con letras del alfabeto como x o y. La segunda materia es la trigonometría, que se encarga de estudiar las razones trigonométricas de seno, coseno, tangente, cotangente, secante y cosecante y es utilizada donde se requiera medir con precisión siendo así muy útil en la arquitectura, astronomía, geografía, ingeniería y por supuesto en la navegación y las telecomunicaciones. Es por eso que en el siguiente blog, se va a tratar acerca de la importancia de estas dos ramas dentro del cálculo, repasando un poco sus generalidades y finalmente viendo sus respectivas aplicaciones y conclusiones de lo que se haya investigado acerca de ellas.
Desarrollo.-
El Álgebra.-
Como definición técnica del álgebra se dice que es una rama de las matemáticas que utiliza no solo números y signos, sino también letras para resolver operaciones. Visto de otro modo, el álgebra busca hallar el valor numérico de variables denominadas incógnitas. Estas se representan mediante letras del alfabeto como x o y.
Además de la definición, mediante el álgebra se resuelven distintos tipos de operaciones como sumas, restas, multiplicaciones, divisiones, y otras más complejas como los logaritmos. Así, en un sentido más amplio, se puede entender al álgebra como el análisis de relaciones, cantidades y estructuras. (Westreicher, 2020)
Importancia del dominio del álgebra.-
es menester tener un dominio previo en el álgebra, ya que dentro de este campo temas como factorización, los sistemas de ecuaciones de n incógnitas, las ecuaciones lineales, ecuaciones cuadráticas, propiedades de los exponentes y sobre todo funciones exponenciales, cuadráticas y logarítmicas son temas de estudio con los que nos vamos a encontrar y para poder dominarlos hay que tener un perfecto conocimiento de estos.
Diferencia ente el álgebra y la trigonometría.-
Algo muy importante de recalcar del álgebra es su diferenciación con la aritmética, ya que en cierto modo Al igual que esta, las operaciones fundamentales del álgebra son adición, sustracción, multiplicación, división y cálculo de raíces. La aritmética, sin embargo, no es capaz de generalizar las relaciones matemáticas, tales como el teorema de Pitágoras, que dice que en un triángulo rectángulo el área del cuadrado de lado la hipotenusa es igual a la suma de las áreas de los cuadrados de lado los catetos.
 |
| Figura 1 |
Así en una expresión como: 12x3
- El signo puede ser positivo (+) o negativo (-), es este caso es positivo.
- El coeficiente es el número que acompaña a la variable, que en este caso sería el 12.
- La variable es la incógnita representada por la letra x.
- El exponente es la potencia a la que esté elevada la variables, que en el ejemplo sería 3. Si no aparece ningún exponente se sobreentiende que es 1.
12x3+4y
Las expresiones pueden expresarse en función al número de términos que las contienen como:
- Monomio: Tiene un término: 15z
- Binomio: Posee dos términos: 2x3-7y
- Trinomio: Tiene tres términos: 3x2+8y+2z
- Polinomio: Cuenta con más de tres términos: 5x2-3y+6z-9
La trigonometría.-
La trigonometría estudia las relaciones que existen entre los lados de un triángulo y sus ángulos, se encarga de estudiar las razones trigonométricas de seno, coseno, tangente, cotangente, secante y cosecante, además de ser utilizada en campos en donde se requiera medir con precisión, La trigonometría es usada especialmente en el estudio de las esferas dentro de la geometría espacial. Entre los usos más comunes de la trigonometría se encuentran la medición de distancias entre estrellas o entre puntos geográficos.
Conceptos importantes en la trigonometría.-
Dentro de la medición de ángulos se encuentran las siguientes tres unidades:
- El radián: mide el ángulo presentado como central a una circunferencia y su medida es igual a la razón entre la longitud del arco que comprende de dicha circunferencia y la longitud del radio, es decir, mide la cantidad de veces que la longitud del radio traza ese determinado arco en la circunferencia (su uso más importante es en las matemáticas).
- El grado sexagesimal: es el ángulo central subtendido por un arco cuya longitud es igual a la tricentésima sexagésima (1/360) parte de una circunferencia. Es la nonagésima (1/90) parte de un ángulo recto(usado para medir tiempos como las horas, minutos y segundos y ángulos (grados) principalmente).
- El sistema decimal: es una técnica de numeración en la que las cantidades se representan utilizando como base aritmética el número diez y sus potencias. Se trata del sistema de uso más común(Utilizado en topografía y en la construcción).
Funciones y razones trigonométricas.-
Dentro de la trigonometría se hace uso de ciertas razones para poder determinar los cocientes entre los lados de un triángulo rectángulo (dos de sus lados) y ángulos que lo conforman, para ello existen seis funciones trigonométricas que se consideran básicas en el punto de partida del estudio de la trigonometría que son: seno, coseno, tangente, cotangente, secante y cosecante, pero para el estudio de la trigonometría se deben recordar el nombre de los lados de un triángulo rectángulo, así que a continuación se los va a ir definiendo.
- Hipotenusa: Se refiere al lado que se encuentra en posición opuesta al ángulo recto (90 grados). Es el de mayor longitud,
- Cateto opuesto: Es el lado que se encuentra contrario al ángulo recto.
- Cateto adyacente: es el lado del triángulo rectángulo que se encuentra contiguo o inmediato al ángulo recto.
 |
| Figura 2: Funciones y razones trigonométricas |
Funciones básicas trigonométricas:
- Seno: el seno de un ángulo se refiere a la relación que existe entre el cateto opuesto y la hipotenusa. Es el cociente que resulta de dividir la medida del cateto opuesto entre la longitud de la hipotenusa.
- Coseno: el coseno de un ángulo es la relación existente entre el cateto adyacente y la hipotenusa, es el cociente resultante de la división entre la longitud del cateto adyacente y la hipotenusa.
- Tangente: el cálculo de la tangente de un ángulo es la división de la medida del cateto opuesto entre la longitud del cateto adyacente.
- Cotangente: es la razón inversa de la tangente. la cual se define como el resultado de la división del cateto adyacente entre al cateto opuesto.
- Secante: la secante es la unión inversa al coseno y resulta de la división de la longitud de la hipotenusa entre el cateto adyacente.
- Cosecante: La cosecante se puede definir como la función opuesta o inversa del coseno que resulta de la división de la hipotenusa entre el cateto opuesto.
 "
"Las matrices se utilizan para múltiples aplicaciones y sirven, en particular, para representar los coeficientes de los sistemas de ecuaciones lineales o para representar las aplicaciones lineales; en este último caso las matrices desempeñan el mismo papel que los datos de un vector para las aplicaciones lineales.
Ejemplo:
Representación Matricial de una transformación R3 en R4
Si se tiene una transformación T: R3 → R4 dada por
Para este caso utilizando el resultado de la transformación, se puede determinar fácilmente la matriz de transformación, separando el vector original y determinando las operaciones que se realizaron.
Aplicación del álgebra en el cálculo.-
Dentro del cálculo el álgebra es de suma importancia, ya que para llegar a una solución de algún problema matemático, las ecuaciones que forman parte del álgebra siempre van a estar presentes dentro de los cálculos en campos como el cálculo por ejemplo, a continuación se puede ver un ejemplo en donde se aplica el álgebra en la resolución de límites algebraicos.
La trigonometría tiene innumerables aplicaciones en diversos campos de la ciencia: de una u otra manera en todos los campos de las matemáticas; en la física, por ejemplo en fenómenos ondulatorios; en la astronomía, por ejemplo para medir distancias entre planetas; en la geodesia, etc.
Ejemplo:
Un ejemplo de la vida real del uso de la trigonometría es el siguiente:
El Canadarm 2, un brazo manipulador robótico gigantesco de la Estación Espacial Internacional. Este manipulador es operado controlando los ángulos de sus articulaciones. Calcular la posición final del astronauta en el extremo del brazo requiere un uso repetido de las funciones trigonométricas de esos ángulos que se forman por los varios movimientos que se realizan.
Aplicación de la trigonometría en el cálculo.-
Dentro del cálculo la trigonometría también se hace presente y nos ayuda mucho en el caso de solución de integrales por ejemplo, las integrales por sustitución trigonométrica.
Las integrales trigonométricas son una parte importante de la técnica de integración llamada sustitución trigonométrica. Esta técnica nos permite convertir expresiones algebraicas que quizás no podamos integrar en expresiones que involucren funciones trigonométricas para poder llegar a la solución de dichas integrales.
Ejemplo:
Integración de ∫ (cosʲx senᴷx) dx donde k es impar
- Se evalúa primeramente ∫cos²x sen³xdx.
- Para convertir esta integral en integrales de la forma ∫cosʲx senxdx, se reescribe sen³x = sen²xsenx y realiza la sustitución.
sen²x = 1 − cos²x. Así,
Después de haberse realizado una investigación de la importancia del álgebra y la trigonometría en el cálculo, habiendo revisado conceptos, aplicaciones y algunos ejemplos se obtuvieron las siguientes conclusiones:
- El álgebra ha influido mucho en la resolución de problemas complejos gracias a la integración de variables que se usan para representar problemas y llegar a una solución.
- Tanto el álgebra como la trigonometría ha ayudado mucho en aspectos de la ciencia, más en el caso de realizar cálculos complejos y de exacta precisión.
- El cálculo depende mucho del uso de expresiones algebraicas para poder hallar soluciones a los ejercicios que se proponen dentro de este campo.
- la trigonometría y el álgebra siempre van a estar presentes para poder resolver problemas relacionados con la vida profesional y la vida diaria.
Bibliografía.-
- Equipo editorial, E. (05 de 08 de 2021). https://concepto.de/trigonometria/.
Obtenido de https://concepto.de/trigonometria/#:~:text=La%20trigonometr%
C3%ADa%20es%2C%20atendiendo%20al,%2C%20cotangente%2C%20secante%20y%20cosecante.
- https://sites.google.com/. (01 de 05 de 2021). Obtenido de https://sites.google.com/site/1451matematica/
segundo-hoja
-khanacademy.org. (01 de 05 de 2022). https://es.khanacademy.org.
Obtenido de https://es.khanacademy.org/computing/computer-programming/programming-natural-
simulations/programming-angular-movement/a/trigonometry
- LINEAL2CX07. (08 de Abril de 2016). Obtenido de https://lineal2cx07.wordpress.com/2016/04/08/
representacion-matricial-de-una-transformacion-lineal/
- Westreicher, G. (28 de 12 de 2020).
Obtenido de https://economipedia.com/definiciones/algebra.html#:~:text=El%20%C3%
A1lgebra%20es%20una%20rama,del%20alfabeto%20como%20x%20o%20y.
- Westreicher, G. (28 de 11 de 2020). Economipedia.com. Obtenido de https://economipedia.com/definiciones/algebra.html#:~:text=El%20%C3%
A1lgebra%20es%20una%20rama,del%20alfabeto%20como%20x%20o%20y.
20descritas%20en%20esta%20secci%C3%B3n.
Por el contrario, el álgebra tiene la capacidad de dar una generalización que cumple las condiciones del teorema: c^2 =a^2 + b^2 , en donde un número multiplicado por sí mismo se denomina cuadrado, y se representa con el superíndice 2.